[게임 AI] A* (에이스타) 알고리즘
개요
길 찾기길 찾기 알고리즘 중 하나인 Astar 알고리즘에 대해 알아보자.
에이스타 알고리즘이란?
출발 지점부터 목표지점까지 주변을 점진적으로 탐색하며 경로를 찾아내는 알고리즘이다.
다익스트라 알고리즘을 확장한 알고리즘으로, 노드에서부터 목표까지의 거리값인 휴리스틱 추정값(H)이 존재한다는 차이점이 있다.
장애물이 고정되어 변화하지 않는다는 전제조건이 있을 때 사용하기 좋으며, 구현이 간단해 여러 형태로 변형하여 구현할 수 있다는 장점이 있다.
구현
에이스타의 구성
에이스타가 어떻게 구성되어 있는지 알아보자
에이스타 알고리즘의 이해를 돕기 위해 사각타일의 격자무늬에서 길 찾기를 한다고 가정해 보자.
하나의 사각타일을 '노드'라고 부를 것이며, 각 노드는 G값, H값, F값을 가지고 있다.
G값은 시작지점부터 현재 노드까지의 거리를 의미하고, H값은 목표지점부터 현재 노드까지의 거리를 의미한다. F값은 G값과 H값의 합을 의미한다.
타일을 탐색할 때 이 값들을 계산한다. G값은 목표를 향해 이동할수록 값이 점점 커지고, H값은 목표와 가까워질수록 점점 줄어든다.
또, 타일은 Open 상태인지 여부와 Close 상태인지 여부를 나타내는 값을 가지고 있다.
Open 상태의 노드는 탐색이 이루어졌으며, 한 번 더 탐색될 수도 있는 노드이다. G, H, F값의 계산이 이루어진 상태이며, 탐색이 추가적으로 될 수 있기 때문에 G, H, F값이 갱신될 여지가 있다.
Close 상태의 노드는 탐색을 마쳤으며, 다시 탐색될 수 없는 노드이다. G, H, F값의 계산이 이루어진 상태이며, 탐색을 마친 노드이기 때문에 G, H, F값이 갱신될 여지가 없다.
오픈리스트는 Open상태인 타일들이 들어가 있는 리스트이다. F값이 가장 낮은 값을 반환해줘야 하기 때문에 우선순위 큐로 구현하는 것이 일반적이다.
에이스타의 수행 순서
에이스타 알고리즘이 어떤 과정을 통해 길을 찾아내는지 알아보자
에이스타는 일련의 루틴을 반복하며 목표를 향해 나아간다.
그 첫 번째는 주변 탐색이다. 시작지점부터 상하좌우, 대각선에 위치한 노드들을 탐색한다. 장애물과 Close상태의 노드는 탐색하지 않는다.
두 번째는 값 세팅이다. 첫 번째 과정을 통해 탐색 한 주변 노드들의 G, H, F값을 세팅한다. 값 세팅이 끝나면 오픈리스트에 넣어야 한다. 오픈리스트에 들어가면 오픈상태이기 때문에 Open이 true로 바뀐다.
세 번째는 다음 노드 설정이다. 두 번째 과정을 통해 오픈리스트에 담긴 노드들 중 F값이 가장 낮은 노드를 뽑아내 그 노드의 주변을 다시 탐색한다.
오픈리스트에서 빠져나온 노드는 Open이 false로 바꾸고, Close가 true가 된다.
초기세팅
이제 위의 과정들을 수행해 보며 어떻게 동작하는지 확인해 보자.
초기 상태의 타일은 인덱스를 제외한 모든 값들이 0으로 맞춰져 있다.

여기에서 0번 인덱스를 시작지점, 14번 인덱스를 목표지점으로 지정한다.
시작지점을 빨간색, 목표지점을 파란색으로 표시한다.
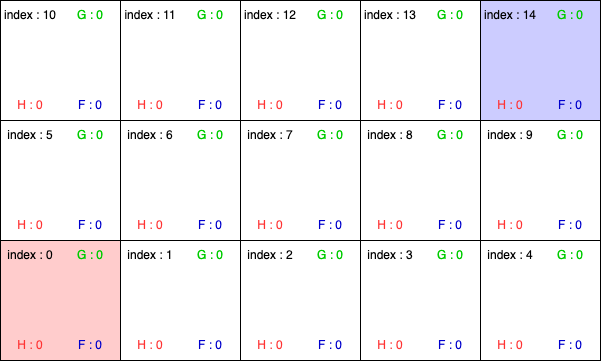
그리고 2번과 7번 인덱스를 장애물로 지정한다.
장애물은 회색으로 표시한다.

주변 탐색
이제 위에 작성한 에이스타의 수행 순서에 맞춰 진행해 보자.
우선 0번째 인덱스의 주변 노드를 탐색한다. 이때 0번째 인덱스는 Close상태가 된다.
현재 노드엔 동그라미 심볼을 추가하였다.

값 세팅
이번엔 탐색한 노드의 값을 세팅하겠다.
H는 현재 노드 기준 목표까지의 가로, 세로로 이동했을 때의 칸수 * 10으로 한다.
G는 자신을 탐색한 노드의 G값에 가로 세로로 이동했을 시, 10을 더하고 대각선으로 이동했을 시, 14를 더한다.
F는 G와 H를 더한다.
이후 오픈리스트에 넣는다.

다음 노드 설정
마지막으로 다음 노드를 설정하겠다. 다음노드는 오픈 상태의 노드들 중 F값이 가장 작은 노드로 선정한다.
여기선 6번 인덱스의 노드가 가장 작으니 6번 노드부터 다시 탐색을 시작한다.
장애물과 마주한 경우
지형 탐색을 해보자. 지형탐색을 좀 더 디테일하게 설명하자면 상하좌우를 먼저 수행한다. 지금은 6번의 오른쪽인 7번 인덱스가 장애물인 상황이다.
상하좌우의 탐색을 마치면 대각선 탐색을 해야 하는데, 대각선을 탐색할 땐 몇 가지 제한사항이 있다. 만약 우측 상단을 탐색하고 싶다면, 우측과 상단이 장애물이 아니어야 한다.
지금 같은 경우엔 7번이 장애물이기 때문에 12번 노드를 탐색할 수 없다. 만약 이런 제한사항을 두지 않는다면, 7번 위치에 벽이 있음에도 7번 벽과 11번 공간사이를 비집고 12번으로 이동하는 모습이 나올 수도 있다.

이미 Open상태인 노드의 값을 세팅하는 경우
0번 인덱스는 Close이기 때문에 탐색하지 않는데, 5번과 1번 인덱스는 이미 탐색이 이루어진 상황임에도 Open상태이기 때문에 다시 한번 탐색을 수행해야 한다.
하지만 탐색을 했다고 해서 무조건 값을 세팅하는 것이 아니다. 지금 5번의 F값은 60이다. 여기서 만약 값을 새롭게 세팅하게 된다면 6번 노드의 G값인 14에서 가로 이동을 했기 때문에 10을 더하면 5번 인덱스의 G값은 24가 되며 기존의 10보다 더 커지게 된다.
이런 경우엔 값을 세팅해선 안된다. 이미 Open상태인 노드의 값 세팅은 무조건 이전 F값보다 세팅 후 F값이 더 작을 때만 발생한다.
때문에 10번, 11번만 값세팅을 한다.

목표를 찾을 때까지 반복
이제 목표를 찾을때까지 반복한다.



목표를 찾고 난 후
목표를 찾고 나면, 목표에서 시작위치까지 이어진 화살표를 역으로 거슬러 올라가면 된다. 이로써 시작위치에서 목적지까지 가는 최단경로를 계산하게 되었다.

코드
필자가 구현한 Astar알고리즘의 일부 코드를 보며 어떻게 구현할 수 있나 생각해 보자. 직접 구현하고 싶다면 보지 않는 것을 추천한다.
노드를 구성하는 요소는 다음과 같다.
어떤 노드가 현재 노드를 계산했는지를 체크하기 위해 Parent 변수를 넣었다. 그 외의 값은 위에 설명했던 그대로이다.
public class AstarTile
{
/// <summary> 타일의 인덱스 </summary>
public int Index { get; private set; }
/// <summary> 목표까지의 대략적인 거리 </summary>
public int H { get; private set; }
/// <summary> 지금까지 이동한 거리 </summary>
public int G { get; private set; }
/// <summary> 목표까지의 거리 + 이동한 거리 </summary>
public int F => H + G;
/// <summary> 오픈 리스트에 있는지 유무 </summary>
public bool IsOpen { get; set; }
/// <summary> 닫힌 상태인지 여부 </summary>
public bool IsClose { get; set; }
/// <summary> 장애물인지 여부 </summary>
public bool IsObstacle { get; set; }
public AstarTile Parent { get; set; }
}길 찾기 위한 과정은 아래와 같다.
설명했던 순서와는 조금 다르다. 현재 노드를 찾고, 주변 노드를 탐색하고, 값 세팅을 한다.
while (openList.Count > 0)
{
// 현재 노드를 찾아낸다. openList에서 F값이 작은 노드를 반환하도록 한다.
// openList는 우선순위 큐로 구현되어 있으며, F값을 기준으로 오름차순으로 정렬되어있다.
curTile = openList.Dequeue();
// 경로를 찾았다면 탈출한다.
if (curTile.Index == destIndex)
{
Debug.Log("Find Path");
break;
}
curTile.IsClose = true;
curTile.IsOpen = false;
// 주변 타일을 탐색한다.
var nearNode = FindNearTile(curTile);
// 오픈 리스트에 넣는다.
// 오픈 리스트에 넣으면서 값계산도 이루어진다.
nearNode.ForEach(tile => AddToOpenNode(tile, curTile));
}주변 노드를 탐색하는 코드는 다음과 같다.
이곳에 사용된 enum 타입인 Direct와 DiagonalDirect를 보기 편하도록 함께 기재하였다.
public enum Direct
{
Start = -1,
Left = 0,
Right = 1,
Up = 2,
Down = 3,
End = 4,
}
public enum DiagonalDirect
{
Start = -1,
LeftUp = 0,
RightUp = 1,
LeftDown = 2,
RightDown = 3,
End = 4,
}
// 상하좌우 방향을 빠르게 찾기 위한 룩업테이블
static readonly int[] dtX = { 0, 0, -1, 1 };
static readonly int[] dtY = { 1, -1, 0, 0 };
static readonly bool[] dirOpen = { false, false, false, false };
// 대각선 방향을 빠르게 찾기 위한 룩업테이블
static readonly int[] dgX = { -1, 1, -1, 1 };
static readonly int[] dgY = { 1, 1, -1, -1 };
static readonly (int, int)[] dgB = {
((int)Direct.Left, (int)Direct.Up),
((int)Direct.Right, (int)Direct.Up),
((int)Direct.Left, (int)Direct.Down),
((int)Direct.Right, (int)Direct.Down)
};
/// <summary> 주변 타일 반환용 리스트. FindNearTile에서만 사용된다. </summary>
private List<AstarTile> nearTileResult = new List<AstarTile>(8);
private List<AstarTile> FindNearTile(AstarTile curTile)
{
nearTileResult.Clear();
int curX = curTile.Index % TileManager.WidthCount;
int curY = curTile.Index / TileManager.WidthCount;
// 상하좌우 검사부터 한다.
for (Direct i = Direct.Start + 1; i < Direct.End; ++i)
{
int index = (int)i;
int x = curX + dtX[index];
int y = curY + dtY[index];
dirOpen[index] = IsOpenableTile(x, y);
if (dirOpen[index]) nearTileResult.Add(tileList[x + y * TileManager.WidthCount]);
}
// 대각선 검사를 한다.
for (DiagonalDirect i = DiagonalDirect.Start + 1; i < DiagonalDirect.End; ++i)
{
int index = (int)i;
int x = curX + dgX[index];
int y = curY + dgY[index];
if (dirOpen[dgB[index].Item1] &&
dirOpen[dgB[index].Item2] &&
IsOpenableTile(x, y)) nearTileResult.Add(tileList[x + y * TileManager.WidthCount]);
}
return nearTileResult;
}오픈리스트에 타일을 넣는 코드는 다음과 같다.
오픈상태가 아니라면 값을 바로 세팅하고, 이미 오픈상태라면 현재 경로가 더 짧은지 비교한 후 값을 세팅한다.
private void AddToOpenList(AstarTile tile, AstarTile parentTile)
{
// 닫혀있거나 장애물이면 오픈노드가 될 수 없다.
if (tile.IsClose || tile.IsObstacle) return;
if (tile.IsOpen)
{
// 이미 오픈리스트에 들어있는 경우.
if (tile.IsShortPath(destX, destY, parentTile, IsDiagonal(parentTile, tile)))
{
// 현재 경로가 더 짧은 경로라면 값을 갱신한다.
tile.SetH(destX, destY);
tile.SetG(parentTile, IsDiagonal(parentTile, tile));
tile.Parent = parentTile;
openList.UpdatePriority(tile, tile.F);
}
}
else
{
tile.SetH(destX, destY);
tile.SetG(parentTile, IsDiagonal(parentTile, tile));
tile.IsOpen = true;
tile.Parent = parentTile;
openList.Enqueue(tile, tile.F);
}
}마치며
길찾기 알고리즘은 에이스타 외에 다양하게 존재한다. 그중 널리 알려져 있으며, 비교적 내용이 쉬운 것이 Astar 알고리즘이다.
내용을 이해하고, 직접 구현해 보면 다른 길 찾기 알고리즘을 이해할 때 크게 도움이 될 것이다.